Research

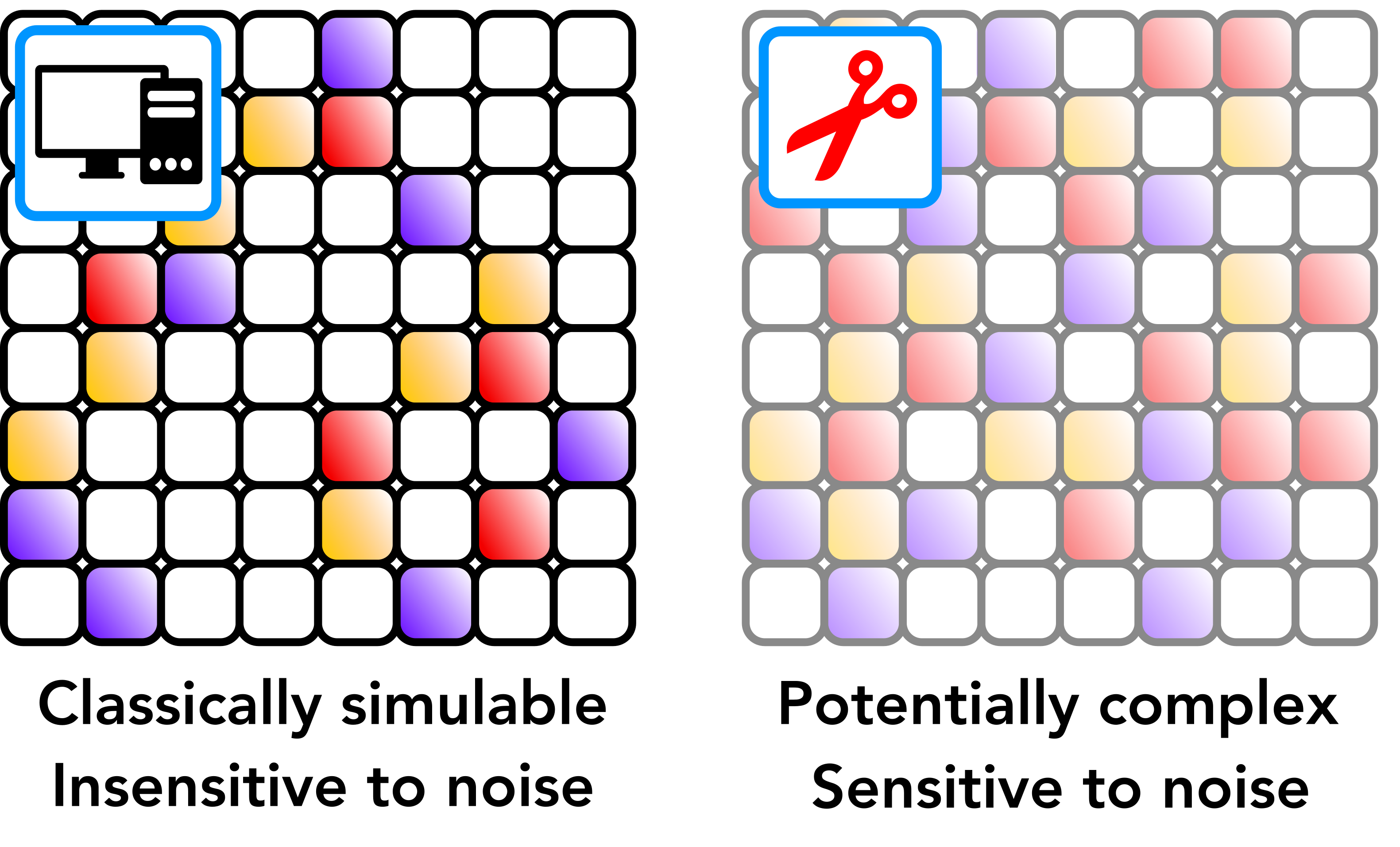
What is the classical complexity of simulating quantum dynamics? Existing results on classical hardness mostly apply to highly-structured, "worst-case" dynamics, while recent numerical methods suggest that "typical" many-body dynamics may in fact be classically easy. In recent work, we make progress on this question by providing a polynomial-time classical algorithm for noisy quantum circuits. This builds in part on an earlier work, in which we showed that noisy many-body quantum systems display universal classes of fidelity decay, controlled by their dispersal of quantum information. I am currently interested in understanding the physics of complexity in noiseless quantum dynamics, and connecting these observations with quantum experiments.

Random unitaries are a key component of several quantum technologies, from quantum device benchmarking to quantum cryptography. They also serve as indispensable toy models for complex processes in quantum many-body physics, quantum machine learning, and quantum gravity. In recent work, we show that local quantum circuits can form random unitaries in exponentially lower circuit depths than previously thought. Our results have widespread applications across theoretical and experimental quantum science. I am currently interested in physically-motivated applications of random unitaries, and in finding quantum advantages in far-from-Haar random dynamics.

The AdS/CFT correspondence posits that certain quantum Hamiltonians are precisely dual to higher-dimensional theories of quantum gravity. This raises a tantalizing possibility: That quantum simulation experiments may one day realize such Hamiltonians, and assist in our understanding of models of quantum gravity. Despite this promise, several concrete challenges remain. In an earlier work, we showed how a novel "many-body" form of quantum teleportation can be used as an experimental litmus test for detecting gravitational dynamics. We demonstrated a toy example of this teleportation in two experiments, and helped to clarify a third realization. In more recent work, we tackle another challenge, by providing a simple and efficient experimental protocol to cool these Hamiltonians to low temperatures, where the gravitational duality applies.

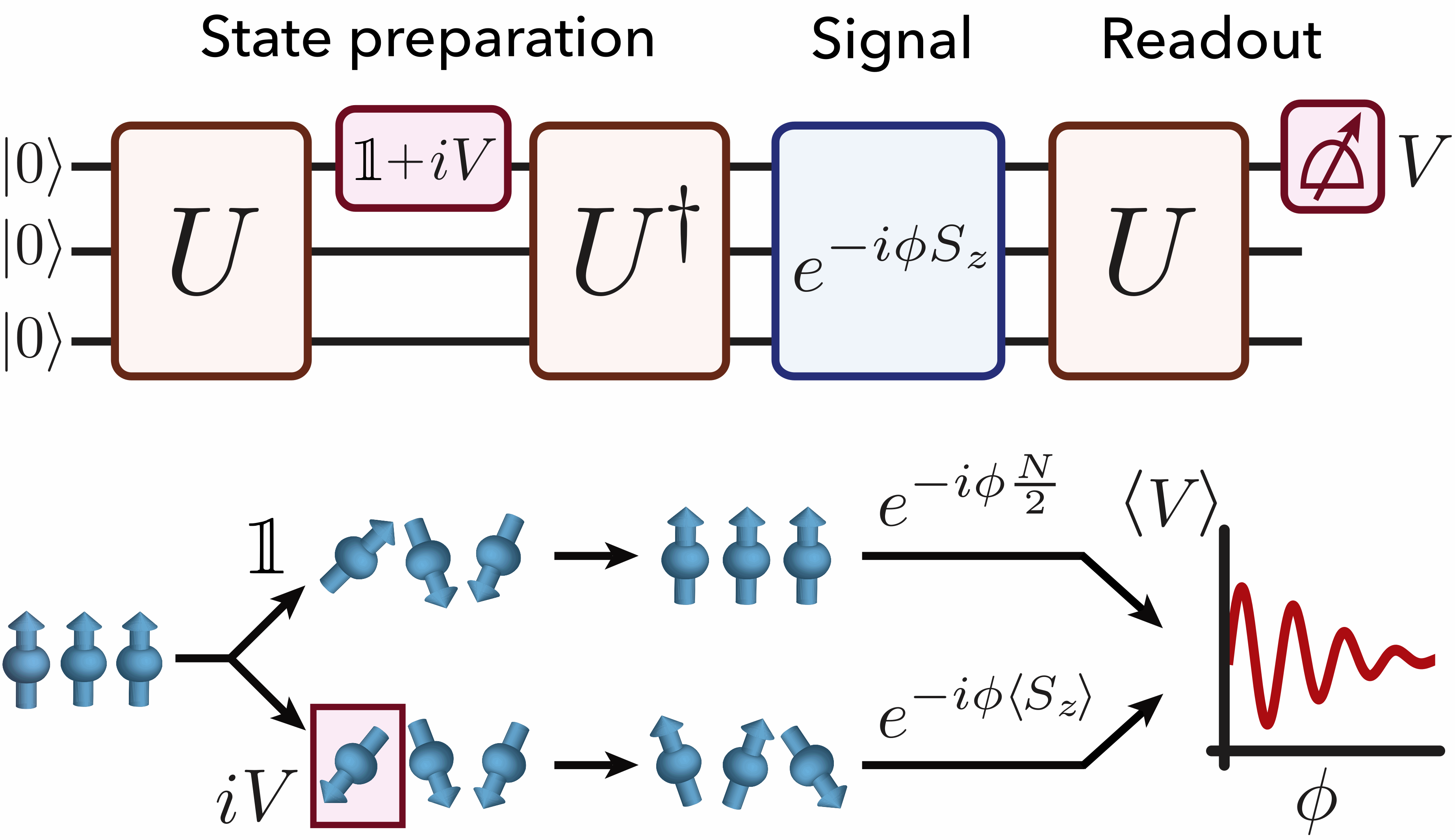
Learning properties of quantum systems can present challenges and opportunities not present in their classical counterparts. My work has intersected this (broad) topic several times. In recent work, we introduced a "universal" protocol for quantum-enhanced sensing of an external field, using solely the dynamics of a generic many-body Hamiltonian. This opens the door to quantum-enhanced metrology in new platforms, such as solid-state spin defects. In a separate work, we showed that learning a many-body Hamiltonian itself at the Heisenberg limit is not possible without a high degree of experimental "control". I also showed how time-reversal protocols can lead to exponential advantages in Hamiltonian learning in several physical scenarios.

In the past, I also worked on novel topological phenomena in atomic, molecular, and optical quantum systems. These systems provide an entirely new physical context for the realization of topological phases, particularly in out-of-equilibrium settings. We predicted and experimentally observed an analogue of non-Abelian statistics in photonic systems; predicted a new, driven phase of topological matter; and provided a toolkit for realizing topological insulators in polar molecule quantum simulators. More recently, we introduced a theoretical framework to characterize the bulk-boundary correspondence in topological stabilizer codes; for example, this allows us to extend known results on 2D stabilizer codes to fracton codes in higher-dimensions.